Probabilistic data structures: Bloom Filters, Count Min Sketch & Skip Lists

Exploring Bloom Filters, Count Min Sketch, and Skip Lists for Big Data and System Design

In the previous article, we covered common data structures in Redis, which led me to investigate their internals. In this post, we’ll explore key probabilistic data structures, including one that serves as the foundation for Redis Sorted Sets.

Why use probabilistic data structures?

Analyzing massive Terabyte-sized datasets is increasingly common in web analytics and online advertising. Traditional methods, like Hadoop and MapReduce, can lead to slow, high-latency processes, making them unsuitable for real-time applications.

While simple metrics, such as total page views or average conversion prices, can be efficiently summarized using daily data or in-stream counters, more complex metrics—like unique visitor counts or the most frequent items—are resource-intensive to compute directly.

The rest of the article will explore three probabilistic data structures that can efficiently handle such complex queries. But first, let’s walk through an example to understand the challenges involved.

Real-world examples of Probabilistic Data Structures

Given a dataset with 10 million integers, where no more than 1 million are distinct (resulting in a 40MB raw dataset size at 4 bytes per integer), here are some key questions we need to address:

• Does the dataset contain a specific element (Membership Query)?

• What are the most frequent elements (heavy hitters or top-k elements)?

• What are the frequencies of those elements?

• How many elements fall within a specific range (Range Query, like SELECT count(v) WHERE v >= c1 AND v < c2 in SQL)?

For the first question, using a sorted list or hash table would need around 4MB space (1M * 4 bytes). This works for smaller datasets, but for datasets that grow into terabytes, it’s not scalable. A probabilistic data structure like LogLogCounter, however, can handle this in just 2KB space!

Sounds interesting, right? Let’s dive into the data structures that help answer each of these questions efficiently.

Read on till the end for a concise comparison between probabilistic and non-probabilistic data structures.

---

---

What are probabilistic data structures?

Probabilistic data structures are designed to efficiently answer the questions mentioned above while optimizing for time and space but with an acceptable margin of error.

In simple terms, non-probabilistic data structures provide exact answers—such as "How many items are there? Exactly 1,600,000"—probabilistic data structures might respond with "How many items are there? Approximately 1,523,425, with a 99% probability."

Types of Probabilistic Data Structures

Bloom Filters

What are bloom filters and why use them?

Bloom filters can estimate if a dataset contains a specific element (Membership Query) in a time-efficient manner. They can return 2 responses:

• If a Bloom filter returns False, the item is not in the set.

• If it returns True, the item might be in the set, but there’s a chance of a false positive (we’ll have a look at why this happens shortly).

How do bloom filters work?

Membership Query using bloom filters

A Bloom filter has two key components:

1. Data structure: A bit array of length n. For example, a bit array of length 10 (with indices 0-9) [Figure 1]

2. Hash functions: There are k hash functions that output an index between 0 and n-1, setting the corresponding bit in the array.

Figure 1: Bit array data structure used in Bloom Filters

Let's see how items are added and looked up in a Bloom filter.

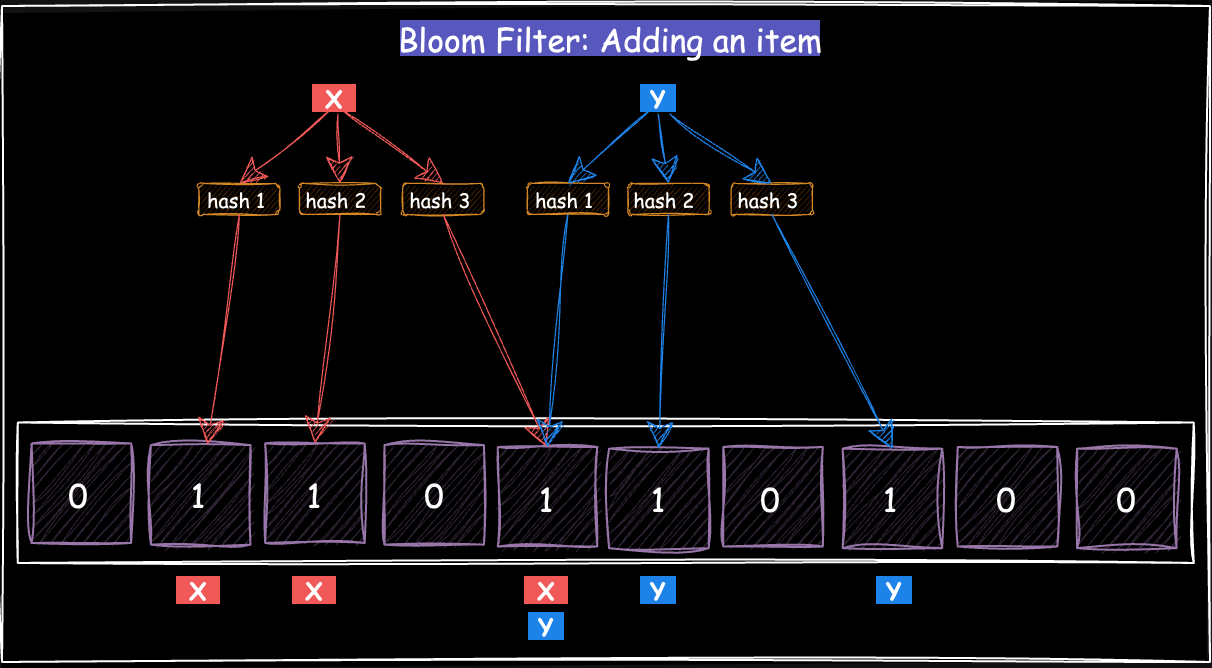
Adding an item

To add an item to a Bloom filter, the following steps are performed:

1. The item is hashed using k hash functions.

2. The modulo operation with the bit array length (n) is applied to the hash outputs to find the positions (buckets) in the array.

3. The bits at these k positions are set to 1.

In Figure 2, the items X and Y are added as follows:

For X:

• hash1(X) mod 10 = 1

• hash2(X) mod 10 = 2

• hash3(X) mod 10 = 4

For Y:

• hash1(Y) mod 10 = 4

• hash2(Y) mod 10 = 5

• hash3(Y) mod 10 = 7

The bucket at index 4 is set to one both the items X and Y.

Figure 2: Adding an item in a Bloom Filter

Looking up an item

To check if an item is present in a Bloom filter, the following steps are taken:

1. The item is hashed using the same k hash functions as during the insert operation.

2. The modulo operation with the bit array length (n) is applied to each hash output to find the corresponding array positions (buckets).

3. The bits at these positions are checked.

   1. If any of these bits are 0, the item is not in the Bloom filter.

   2. If all bits are 1, the item might be in the Bloom filter due to potential hash collisions or bits set by other items.

Examples (Figure 3 & Figure 4):

For Y (existing item)

• hash1(Y) mod 10 = 4

• hash2(Y) mod 10 = 5

• hash3(Y) mod 10 = 7

Since all the bits at these positions are 1, Y might be in the filter.

For Z (item that doesn’t exist)

• hash1(Z) mod 10 = 3

• hash2(Z) mod 10 = 5

• hash3(Z) mod 10 = 8

Since the bits at positions 3 and 8 are 0, Z is not in the Bloom filter.

Figure 3: Looking up “existing” item in Bloom Filter

Figure 4: Looking up “non-existent” item in Bloom Filter

False Positives

In Figure 5, the Bloom filter is queried to check if F is a member. The following calculations are made:

• hash1(F) mod 10 = 2

• hash2(F) mod 10 = 4

• hash3(F) mod 10 = 7

Bits at positions 2, 4, and 7 are set, indicating that item F might be present. However, this is a false positive because X and Y have set those bits. Therefore, F is not a member of the Bloom filter, illustrating the inherent uncertainty and possibility of false positives in Bloom Filters.

Figure 5: False positives in Bloom Filter

Time & Space Complexity of bloom filters

Bloom filters are more efficient than hash sets for large data lookups due to their constant time and space complexity.

• Time Complexity: O(k) to add and lookup an element, where k is the number of hash functions.

• Space Complexity: Constant space usage, as Bloom filters utilize a fixed number of bits. Each item contributes only a few bits, and bits are reused. Notably, Bloom filters do not store actual values.

Practical use cases of Bloom Filters

The bloom filters are useful in high-ingestion systems to prevent expensive disk seeks. Few applications of bloom filters

• Reducing disk lookups for the non-existing keys in a database

• Determining whether a user ID is already taken

• Filtering out previously shown posts on recommendation engines

• Checking words for misspellings and profanity with a spellchecker

• identifying malicious URLs, blocked IPs, and fraudulent transactions

• Log-structured merge tree (LSM) storage engine used in databases such as Cassandra uses a bloom filter to check if the key exists in the SSTable

• MapReduce uses the bloom filter for the efficient processing of large datasets

Bloom filter calculator

hur.st bloom filter calculator can be used to choose the optimal size for the bloom filter and explore how the different parameters interact. The accuracy of the bloom filter depends on the following:

• number of hash functions (k)

• quality of hash functions

• length of the bit array (n)

• number of items stored in the bloom filter

---

Count-Min Sketch: Efficient frequency counting

What are bloom filters and why use them?

A Count-Min Sketch (CMS) is a data structure specifically optimized for two scenarios without the need to store the actual elements:

1. Estimating the frequency of elements in a stream

2. Identifying heavy hitters

CMS utilizes a 2-D array of size w x d (width × depth) [Figure 6], where w represents the number of counters in each row and d denotes the number of rows. Each row is associated with its hash function.

Figure 6: 4 x 3 (w x d) 2D array representing a Count Min Sketch

How does a count-min sketch work?

A. Frequency Estimation using count-min sketch

Adding an item

1. The item is hashed using d independent hash functions. Each hash function corresponds to one row in the 2D array and maps the element to one of the w counters in that row.

2. For each hash function, increment the counter at the corresponding position in the array.

Figure 7 shows the counters of each position after the items X and Y are added to the CMS:

For X:

• hash1(X) mod 4 = 2

• hash2(X) mod 4 = 3

• hash3(X) mod 4 = 1

For Y:

• hash1(Y) mod 4 = 3

• hash2(Y) mod 4 = 3

• hash3(Y) mod 4 = 2

The counters at the above positions in the corresponding rows are incremented by 1.

Figure 7: Adding an item in Count Min Sketch

Querying an item’s frequency

1. Apply the same d hash functions to the query item.

2. Find the counter at the corresponding position in its row for each hash function. The estimated frequency of the element is the minimum value of these counters.

Figure 8 shows how the frequency of an item X is determined:

• hash1(Y) mod 4 = 2 (counter = 1)

• hash2(Y) mod 4 = 3 (counter = 2)

• hash3(Y) mod 4 = 1 (counter = 1)

The estimated frequency of Y is min(1, 2, 1) = 1.

Figure 8: Querying an item in Count Min Sketch

Time & Space Complexity of count-min sketch

• Time Complexity: O(d), where d is the number of hash functions (or rows).

• Space Complexity: O(w × d).

B. Heavy Hitters using count-min sketch

CMS combined with a heap can efficiently identify heavy hitters/elements with frequencies greater than k% of the total dataset size (N). The approach is simple:

1. Initialize a CMS to track the frequency of elements and an empty heap to store the top elements. Set a counter N to track the total number of processed elements.

2. For each new element, update the CMS and estimate its frequency. If the frequency exceeds k x N, add the element to the heap.

3. Periodically prune the heap by removing elements that no longer meet the k x N frequency threshold.

C. Range queries using count-min sketch

An array of Count-Min Sketches can also handle Range Queries (eg: SQL query "SELECT count(v) WHERE v >= c1 AND v < c2), though I won't go into detail here as it's outside the focus of this article.

This is mainly relevant when designing systems like Databases (eg: Clickhouse), Analytics tools (eg: Mixpanel), or Metrics platforms (eg: Grafana). If you're interested in learning more, I've included references at the end for further reading.

Practical use cases of Count-Min Sketch

• Network Traffic Monitoring: Estimate the frequency of IP addresses in a traffic stream.

• Data Streams: Track word counts in massive text streams (e.g., search query trends).

• Approximate Counting in Distributed Systems: Manage resource usage and limit counters in large-scale systems where exact counting is expensive.

---

Skip List

What are skip lists & why use them?

A Skip List is a probabilistic data structure that provides an alternative to balanced trees (self-balancing BST and AVL trees). It uses multiple linked lists to represent different "levels" of the dataset, allowing for fast lookups, insertions, and deletions with logarithmic time complexity.

Figure 9 shows the representation of a SkipList.

There are multiple levels, with each level containing a subset of elements from the previous one, also in sorted order. While it may look like nodes appear multiple times, like Node 5 being in all three levels, it's the same node connected across different levels. For example, Node 5 connects to Nodes 24, 15, and 7 at various levels.

Figure 9: Skip List data structure

How do skip lists work?

Let’s have a look at various CRUD scenarios in a Skip List

Adding an item

The gif in Figure 9 explains this scenario:

1. Start at the topmost level and move forward through the list until you find a node larger than the element to be inserted.

2. Drop down to the next level and continue searching from that position, repeating this process until you reach the base level.

3. Insert the element at the correct position in the base level.

4. Flip a coin to decide if the element should be promoted to the next higher level.

5. If the coin returns heads, insert the element at the same position in the higher level, repeating the promotion and insertion process.

6. Stop promoting the element when the coin returns tails, finishing the insertion process.

Figure 10: Adding an item in Skip List

Querying an item

The gif in Figure 11 explains how an item is queried in a SkipList:

1. Start at the topmost level and move forward, comparing each node’s value with the target.

2. If a larger node is found without matching the target, drop down to the next level and resume the search.

3. Continue this process at each level, moving down and checking nodes until you reach the base level.

4. Stop if the target is found at any level, otherwise the search concludes at the base level. If the target is still not found, it is not in the skip list.

Figure 11: Searching an element in Skip List

Deleting an item

Figure 12 illustrates deletion of an item from a SkipList:

1. Traverse the list at the topmost level to find the node just before the element to be deleted.

2. Drop to lower levels from the current node, continuing to search for the node before the target element.

3. At each level where the element exists, update pointers to bypass and unlink the target node.

4. Once the element is removed from all levels, the deletion is complete.

Figure 12: Deleting an item from Skip List

Time and Space Complexity of a skip list

• Time Complexity:

  • Average Case: The level of a node is determined by coin flips and fewer nodes appear on higher levels. This results in the average time complexity of O(log n) for most operations, as only a few levels need to be traversed.

  • Worst Case: Although rare, coin flips can create an unbalanced skip list where most nodes are concentrated in just 1 or 2 levels, leading to a worst-case time complexity of O(n).

• Space Complexity: O(n), where n is the number of elements.

Use cases of skip lists

Skip lists are useful for fast lookups in large datasets. Some practical use cases include:

• In-Memory Databases: Used for indexing and maintaining sorted data with fast insertions and lookups.

• Priority Queues: Efficiently manage dynamically changing priorities.

• Redis Sorted Sets: Skip lists are the underlying data structure in sorted sets.

---

---

References for reading on probabilistic data structures

• https://highlyscalable.wordpress.com/2012/05/01/probabilistic-structures-web-analytics-data-mining/

---

---

Conclusion

The table in Figure 13 quickly compares commonly used probabilistic data structures, highlighting their use cases, error rates, and memory consumption.

It's worth noting that LogLog Counter and Stream-Summary are two additional probabilistic data structures, which we will explore in detail later.

Figure 13: Comparison matrix of probabilistic data structures

---

Thanks for reading!

Liked this article? Make sure to 💙 click the like button.

Feedback or addition? Make sure to 💬 comment.

Know someone who would find this helpful? Make sure to 🔁 share this post.